This is a short movie on differentiation from first principles. The process of finding the derivative f-x is equal to the limit as h approaches zero of f, of x plus h, minus f of x, divided by h, is called differentiation from first principles.. Now try some questions for yourself. The answers to these questions are on the next slide. Thanks.. This is the definition, for any function y = f (x), of the derivative, dy/dx. NOTE: Given y = f (x), its derivative, or rate of change of y with respect to x is defined as. Example. Suppose we want to differentiate the function f (x) = 1/x from first principles. A sketch of part of this graph shown below.

Differentiation from First Principles YouTube

How to Differentiate by First Principles

Differentiation from first principles YouTube

Differentiation from First Principles a simple explanation of how it works YouTube

Differentiation 1 eg. 2.2 First principles YouTube

Differentiation From First Principles YouTube

Derivative by First Principle for Rational Function YouTube

ten Differentiation from first principles YouTube

How to Find the Derivative of a^x from First Principles YouTube

Differentiation from First Principles Teaching Resources
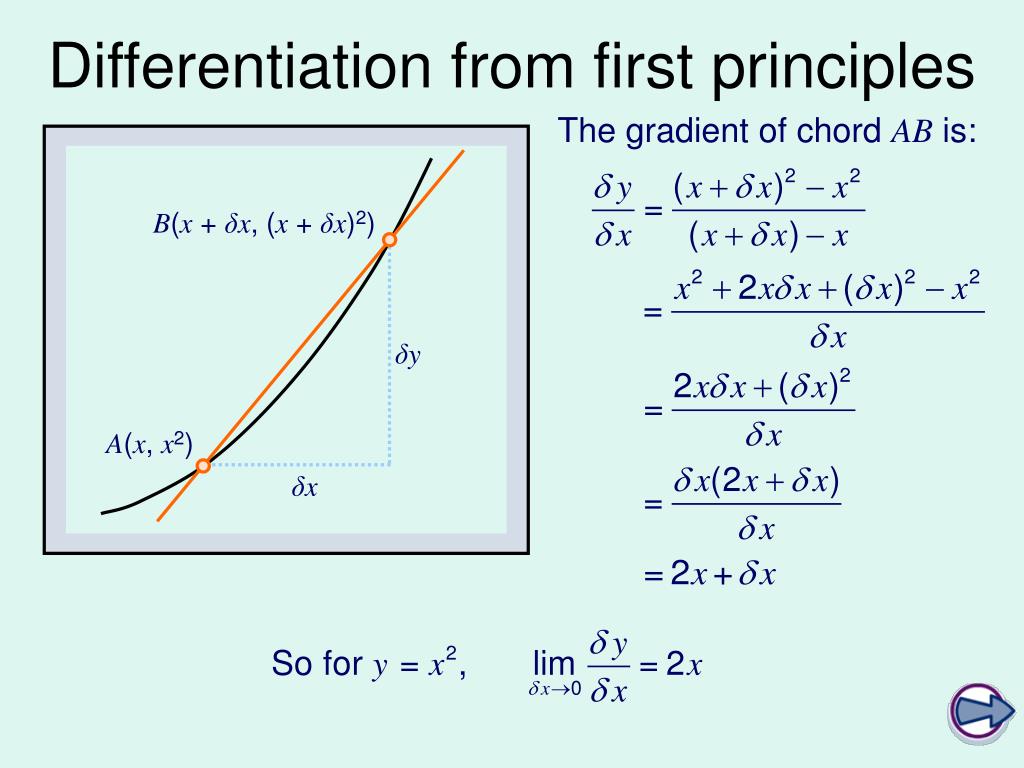
PPT C1 Differentiation from First Principles PowerPoint Presentation ID1806096

The Ultimate List 50 Strategies For Differentiated Instruction

AH Differentiation 1 First Principles YouTube

SPM (Add Maths) Differentiation by First Principle Rule YouTube
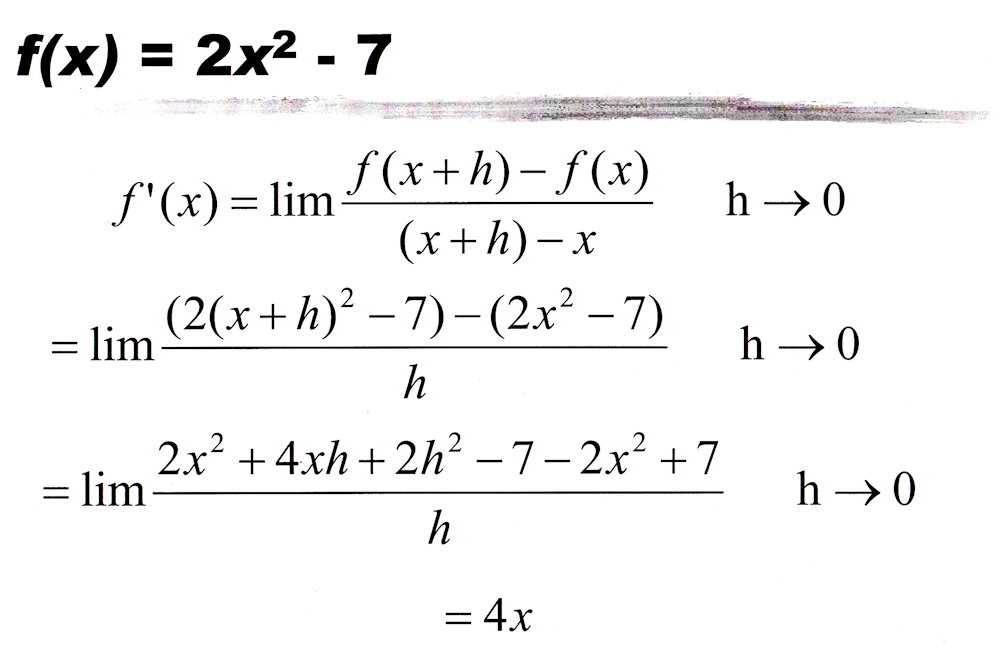
Differentiation Online Exercises
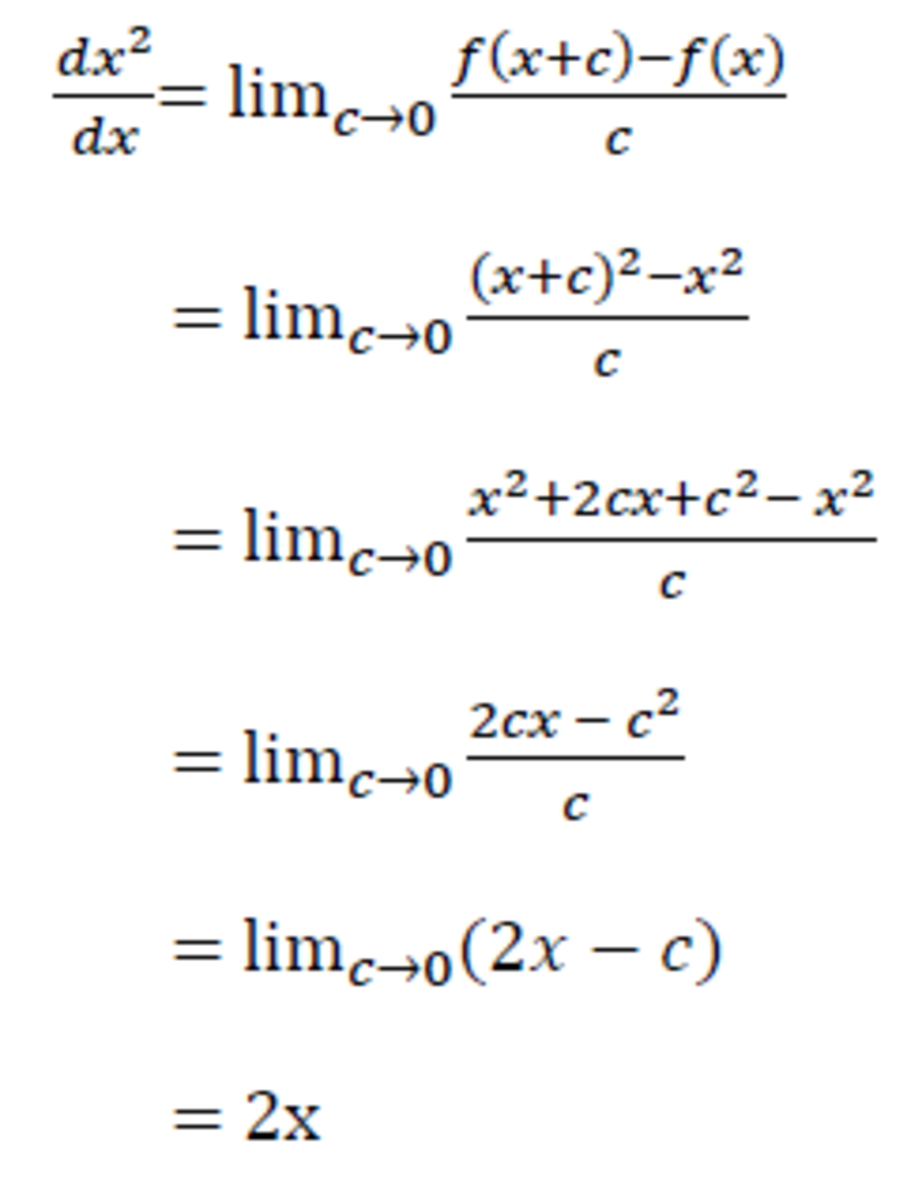
How to Differentiate From First Principles Owlcation

Differentiating from first principles YouTube
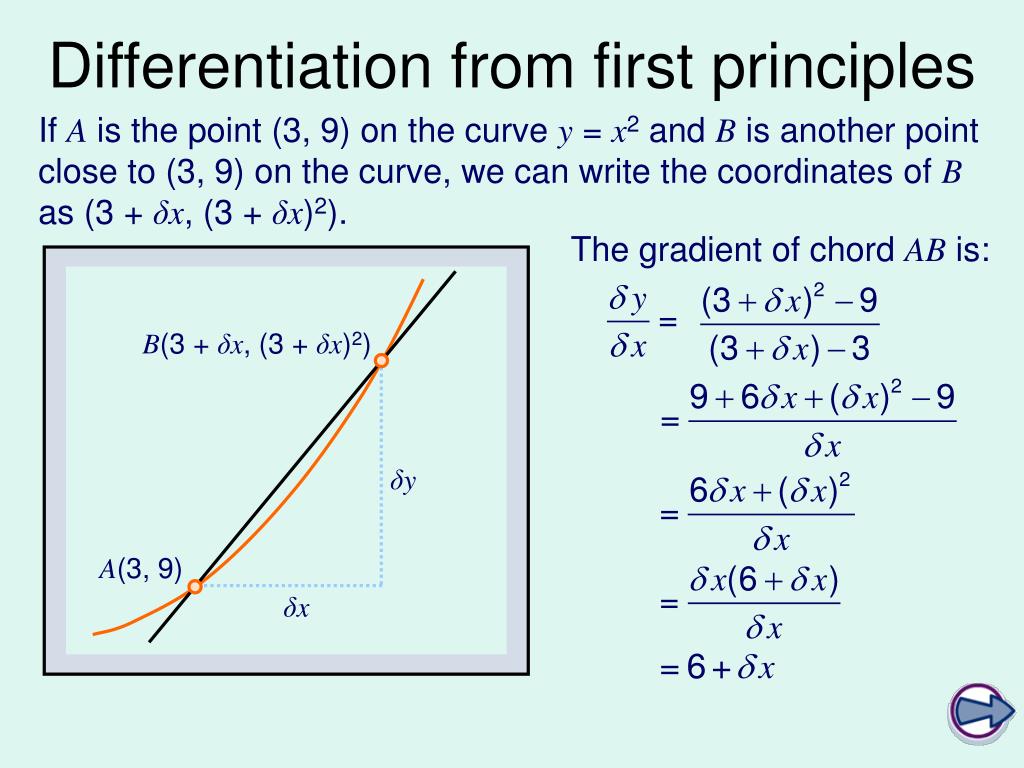
PPT C1 Differentiation from First Principles PowerPoint Presentation ID1806096

A level MATHs Differentiation from first principles questions and problems Edexcel MEDIUM
Math12 CHAPTER 2 DIFFERENTIATION
Most of the time you will not use first principles to find the derivative of a function (there are much quicker ways!). However, you can be asked on the exam to demonstrate differentiation from first principles. Make sure you can use first principles differentiation to find the derivatives of kx, kx 2 and kx 3 (where k is a constant).. Differentiation from First Principles Example Questions. Question 1: For f (x) = x, prove that the gradient is fixed at 1, using first principles. [2 marks] A Level AQA Edexcel OCR. Question 2: Prove that, for any constant c where y = c, the gradient \bigg (\dfrac {dy} {dx}\bigg) is 0, using first principles. [2 marks]

